[Python] 보급로 (SWEA 1249번 파이썬)

https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV15QRX6APsCFAYD&

SW Expert Academy

2차 세계 대전에서 연합군과 독일군의 전투가 점점 치열해지고 있다.

전투가 진행중인 지역은 대규모 폭격과 시가전 등으로 인해 도로 곳곳이 파손된 상태이다.

그림 1(a)에서와 같이 도로들은 전투로 인해 트럭이나 탱크와 같은 차량들이 지날 갈 수 없다.

전투에서 승리하기 위해서는 기갑사단과 보급부대가 신속하게 이동하기 위한 도로가 있어야 한다.

공병대는 출발지(S) 에서 도착지(G)까지 가기 위한 도로 복구 작업을 빠른 시간 내에 수행하려고 한다.

도로가 파여진 깊이에 비례해서 복구 시간은 증가한다.

출발지에서 도착지까지 가는 경로 중에 복구 시간이 가장 짧은 경로에 대한 총 복구 시간을 구하시오.

깊이가 1이라면 복구에 드는 시간이 1이라고 가정한다.
 

                                             그림 1 (a) 파손된 도로                                                             (b) 지도 형태와 이동 방향

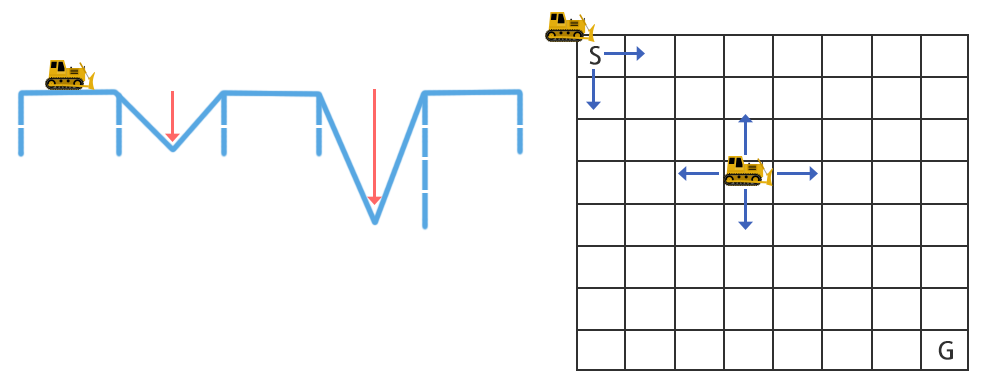
지도 정보는 그림1(b)와 같이 2차원 배열 형태로 표시된다.

출발지는 좌상단의 칸(S)이고 도착지는 우하단의 칸(G)가 된다.

이동 경로는 상하좌우 방향으로 진행할 수 있으며, 한 칸씩 움직일 수 있다.

지도 정보에는 각 칸마다 파여진 도로의 깊이가 주어진다. 현재 위치한 칸의 도로를 복구해야만 다른 곳으로 이동할 수 있다.
 

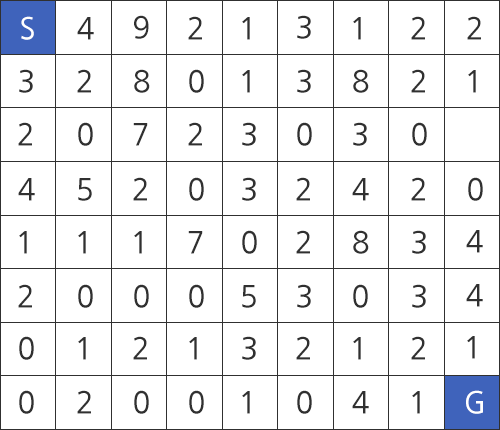
그림 2 지도 정보

이동하는 시간에 비해 복구하는데 필요한 시간은 매우 크다고 가정한다.

따라서, 출발지에서 도착지까지 거리에 대해서는 고려할 필요가 없다.

지도 정보는 그림2에서 보듯이 2차원 배열의 형태이다.

출발지(S)와 도착지(G)는 좌상단과 우하단이 되고 입력 데이터에서는 0으로 표시된다.

출발지와 도착지를 제외한 곳이 0인 것은 복구 작업이 불필요한 곳이다.

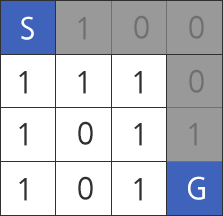
다음과 같은 지도에서 복구 작업 시간이 최소인 시간은 2이고 회색으로 칠해진 경로가 된다.
 

[입력]

가장 첫 줄은 전체 테스트케이스의 수이다.

각 테스트 케이스마다 지도의 크기(N x N)가 주어진다. 지도의 크기는 최대 100 x 100이다.

그 다음줄 부터 지도의 크기만큼 2차원 배열 형태의 지도 정보가 주어진다.
 
[출력]

각 테스트 케이스의 답을 순서대로 출력하며, 각 케이스마다 줄의 시작에 “#C”를 출력하여야 한다.

이때 C는 케이스의 번호이다.

같은 줄에 빈 칸을 하나 두고, 주어진 입력에서 출발지에서 도착지까지 가는 경로 중에 복구 작업에 드는 시간이 가장 작은 경로의 복구 시간을 출력하시오.

 

---

 

 

최단거리를 찾는 일반적인 BFS문제처럼 접근했다가, 해결이 안돼서 다른 분의 풀이를 참고해서 해결했습니다.

2차원 배열의 0,0 지점에서 우측 하단까지 이동하는 최소 시간을 출력해야 합니다.

 

일반적으로 BFS에서 사용하는 방문처리와 다르게, visited 2차원 배열에 현재 칸 까지의 최소 거리를 누적합니다.

방문처리를 진행하지 않는 이유는, 이미 지나간 길이라고 하더라도 다른 길에서 그 지점까지 오는 길이 더 최소일 수 있기

때문입니다.

 

 

이 아이디어까지는 떠올렸는데, 구체적으로 이를 어떻게 구현할지에 대해서 여러 방향으로 생각하다가 시간을 너무 많이 소모해서 결국 답을 찾아봤습니다.

 

 

이미 몇 번의 탐색이 진행 됐다고 가정한 상황에서, 현재 칸을 기준으로 다음 칸을 탐색합니다.

다음 칸(상하좌우)이 이미 한번 지나간 길이라고 하더라도,

다음 칸에 도착했을 때의 시간(현재까지 온 시간 + 다음칸 시간)이 이전에 지나갔을 때의 시간보다 적다면, 갱신해줍니다.

 

만약 이전에 지나간 적이 없다고 하더라도, 최초에 visited(각 칸의 누적 시간)배열을 최댓값인 10000으로 설정했기 때문에,

갱신이 됩니다.

다음 탐색에서 이 칸을 또 지나더라도 현재까지 기록된 최소 시간보다 많이 소모되면 갱신은 이뤄지지 않습니다.

 

이렇게 최소 소모값 갱신이 일어나는 경우에만 큐에 넣어서, 탐색을 이어갑니다.

 

 

visited를 비용 누적으로 만드는 아이디어까지는 떠올렸는데, visited의 모든 칸을 10000으로 설정하고 들릴 때마다 갱신이 되게끔 하는 아이디어까지는 미처 생각하지 못했습니다.

 

 

코드

#swea 1249 보급로
from collections import deque

def bfs(x,y,graph,visited):
    q = deque()
    q.append((x,y))
    min_dist = 10000 #입력의 최댓값이 100^2
    while q:
        x,y= q.popleft()
        dx = [-1,0,1,0]
        dy = [0,1,0,-1]
        for i in range(4):
            nx = x + dx[i]
            ny = y + dy[i]
            if 0<= nx < n and 0<= ny < n: #이미 방문했던 곳이 지금까지 온거 + 다음 칸보다 크면
                if visited[nx][ny] > visited[x][y] + graph[nx][ny]:
                    visited[nx][ny] = visited[x][y] + graph[nx][ny]
                    q.append((nx,ny))
    return min_dist


T = int(input())
for t in range(1,T+1):
    n = int(input())
    graph = []
    for i in range(n):
        arr = list(input())
        arr = list(map(int, arr))
        graph.append(arr)

    visited = [[10000]*n for _ in range(n)]
    visited[0][0] = 0
    bfs(0,0,graph,visited)
    answer = visited[n-1][n-1]
    print(f"#{t}", answer)